Freely floating objects on a fluid governed by the Boussinesq equations

G. Beck, D. Lannes, Ann. IHP/Analyse non linéaire, to appear Download

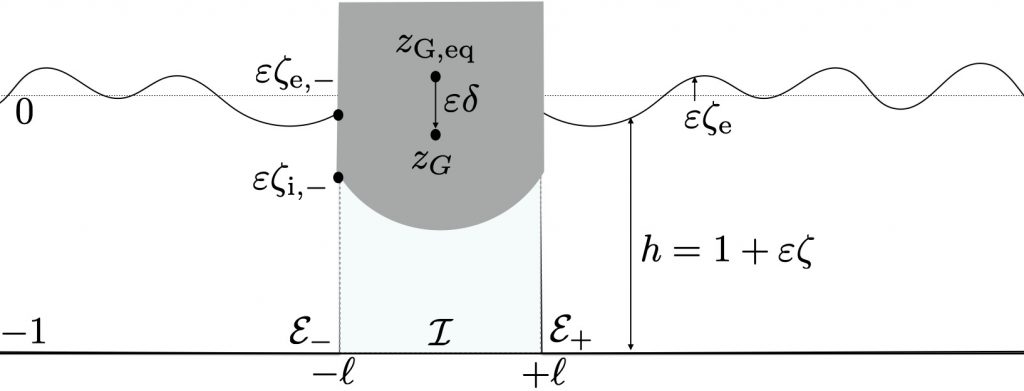
We investigate here the interactions of waves governed by a Boussinesq system with a partially immersed body allowed to move freely in the vertical direction. We show that the whole system of equations can be reduced to a transmission problem for the Boussinesq equations with transmission conditions given in terms of the vertical displacement of the object and of the average horizontal discharge beneath it; these two quantities are in turn determined by two nonlinear ODEs with forcing terms coming from the exterior wave-field. Understanding the dispersive contribution to the added mass phenomenon allows us to solve these equations, and a new dispersive hidden regularity effect is used to derive uniform estimates with respect to the dispersive parameter. We then derive an abstract general Cummins equation describing the motion of the solid in the return to equilibrium problem and show that it takes an explicit simple form in two cases, namely, the nonlinear non dispersive and the linear dispersive cases; we show in particular that the decay rate towards equilibrium is much smaller in the presence of dispersion. The latter situation also involves an initial boundary value problem for a nonlocal scalar equation that has an interest of its own and for which we consequently provide a general analysis.